積分 の 平均 値 の 定理

時計 電池 交換 した の に 止まる積分の平均値の定理とその2通りの証明 | 数学の景色. 積分の平均値の定理の証明. 最大値・最小値定理と中間値の定理を用いた証明. 微分の平均値の定理を用いた証明. 積分 の 平均 値 の 定理その他の平均値の定理. 積分 の 平均 値 の 定理微分における平均値の定理. コーシーの平均値の定理. 積分の平均値の定理. fは [a,b]上積分可能で，m le f(x) …. 積分の平均値定理と微分積分学の基本定理 - 新米夫婦のふたりごと. 平均値の定理 - Wikipedia. 積分 の 平均 値 の 定理定積分に関する平均値の定理 | 関数の積分 | 微分積分 | 数学 . 定積分に関する平均値の定理. を満たす実数 を端点とする有界な閉区間 上に定義された関数 が 上で連続である場合、 の における平均値を、 と定義しました。. 変数 の値 …. 積分の平均値の定理 - kochi-tech.ac.jp. [ 積分の平均値の定理] f(x) がa 5. f(c) = 5 bで連続なとき. 積分 の 平均 値 の 定理b. f(x)dx (a < c < b) b − a Z a. となる数c がa とbの間に存在する。 < 証明> − 23 −. 積分 の 平均 値 の 定理5 x 5 b の範囲でf(x) の最大値をM, …. 積分型の平均値の定理 | 教えて数学理科. ・積分型の平均値の定理. 積分 の 平均 値 の 定理(積分の平均値の定理) 区間 a≦x≦b ( a<b) で 連続 な関数 f (x) について. displaystyleint_ {a}^ {b}f (x)dx= (b-a)f (c) (a<c<b) を満たす …. 積分 の 平均 値 の 定理微分積分学 I{6 平均値の定理 - 名古屋大学. 平均値の定理. 微分積分学I{6. Jacques Garrigue, 2019 年5 月28日. 極値. 積分 の 平均 値 の 定理f(x) がx = c で極大とは, 開区間; c J. 積分 の 平均 値 の 定理J; x = c. 積分 の 平均 値 の 定理f(x) < f(c) 同様に極小とはは, 開区間; c J. J; x = c. f(x) > …. 積分の平均値の定理とその証明 - gamecorder. 積分の平均値の定理. 積分の平均値について、以下の積分の平均値の定理が成り立ちます。 関数 f (x) f ( x) が区間 [a,b]で連続ならば. f (c)= 1 b−a ∫ b a f …. ラグランジュの平均値の定理 | 関数の微分 | 微分積分 | 数学 . 平均値の定理の活用例：瞬間変化率と平均変化率が一致する時点の存在. 平均値の定理の活用例：リプシッツ関数であることの判定. 積分 の 平均 値 の 定理演習問題. 関連知識. …. 第11回 積分の第1平均値の定理、第2平均値の定理 - ねこ騙し数学. 定積分の平均値の定理. f (x) が [a,b] で連続ならば、 が存在する。 定積分の第1平均値の定理. f (x) が閉区間 [a,b] で連続、 g (x) が [a,b] で非負連続ならば、 …. 積分 の 平均 値 の 定理微分積分・中間値と平均値の定理|湘南理工学舎. （関数の曲線はなめらかで、切れ目がないこと） 平均値の定理はいくつかあり、ここでは一般的な「平均値の定理 すなわち ラグランジュの平均値の定理」 …. 積分 の 平均 値 の 定理①「積分の平均値の定理」の証明 大学での積分(リーマン積分 . 第1回目は「積分の平均値の定理」を、高校数学と大学数学の2通りの仕方で証明していきます。 高校数学での証明微分型の平均値の定理と、「不定積分＝ …. 中間値の定理と平均値の定理|京極一樹の数学塾. 積分 の 平均 値 の 定理積分の平均値の定理の証明は、「1999年京大理系後期6」の前半に含まれています。 中間値の定理・平均値の定理. [B]中間値の定理・平均値の定理の問題（2013年日大／ …. 「平均値の定理を証明しよう！」【解析学の基礎シリーズ】1 . 平均値の定理のイメージ. 交通 規則 を 守る

ストナリニ s 風邪 に 効く平均値の定理の明示とその証明. 平均値の定理の証明の発想. 結. 本記事の内容. 本記事は平均値の定理のイメージとその証明を与 …. 積分 の 平均 値 の 定理平均値の定理とその応用 (証明付) - 理数アラカルト. したがって、 平均値の定理は次のように解釈できる。 すなわち、 関数 f(x) f ( x) が区間 [a,b] [ a, b] で連続で、 区間 (a,b) ( a, b) で微分可能な場合には、 二つの点 (a,f(a)) ( a, …. ロルの定理，平均値の定理とその証明 | 高校数学の美しい物語. 平均値の定理の証明のための定理という感じです。 証明. f (x) f (x) が区間内で定数関数のとき. a < c < b a < c < b なる任意の c c で f (c)=0 f ′(c) = 0 とな …. 微分積分学の第1基本定理 | 関数の積分 | 微分積分 | 数学 | ワイズ. 定積分に関する平均値の定理. 関数の片側極限（右側極限・左側極限） 関数の原始関数と不定積分. 微分積分学の第2基本定理（求積分定理） ベクトル値関 …. 平均値の定理の意味・証明・応用例題2パターン | 高校数学の . 平均値の定理は一見複雑ですが，「傾き」という図形的な意味を考えれば理解しやすいです。平均値の定理の式 f (b) − f (a) b − a = f ′ (c) dfrac{f(b)-f(a)}{b …. 平均値の定理 - Wikiwand. 微分積分学 における 平均値の定理 （へいきんちのていり、 英: mean-value theorem ）または 有限増分の定理 ( 仏: Théorème des accroissements finis) は、 実函数 に対 …. 「コーシーの第二平均値定理を証明しよう！」【解析学の基礎 . コーシーの第二平均値定理のを知る意味は？ コーシーの第二平均値定理のイメージ. コーシーの第二平均値定理の明示とちょっとした説明. 証明の発想. い …. 平均値の定理まとめ（証明・問題・使い方） - 理系ラボ. 積分 の 平均 値 の 定理1. 平均値の定理について. つながる機器の保険

ペンギン を 飼う1.1 平均値の定理とは. 平均値の定理とは、以下のことを指します。 区間([a,b])で連続、((a,b))で微分可能な関数(f(x))について. …. 平均値の定理とは？使い方を例題でわかりやすく解説！ - 受験辞典. 平均値の定理は、 曲線の傾きの平均と、曲線上の 1 点における傾きに関して成り立つ定理 です。 開区間 (a, b) で微分可能かつ x = a, b で連続な関数 f(x) …. 定理 - Wikipedia. 微分積分学の基本定理 ロルの定理 平均値の定理 有限生成アーベル群 ゲーデルの不完全性定理 ツォルンの補題 ラグランジュの定理 フェルマーの小定理 オイラーの定理 ケ …. 【t検定】t分布を用いた母平均の検定｜概要・やり方を分かり . 第14章では、 「t検定」 について解説します。. 仮説検定の具体的な例題を解いていきましょう。. 初学者も理解しやすいように丁寧に解説しているので、ぜひ最後ま …. 令和の一橋後期数学 -2024年- - ちょぴん先生の数学部屋. 先日行われた2024年度の一橋大学の後期数学を解いてみました。 ※一橋の後期は文系向けにも関わらず数Ⅲが出題範囲に含まれています。なので、どうしても …. 統計準1級 第8章 統計的推定の基礎 解説｜Kai_lazykoala. 積分 の 平均 値 の 定理この章の目的 : 何が優れた推定量なのかを学ぶ 例えば推定量の1つに最尤推定量があるが 「なんで最尤推定量を用いるのか」 そもそも推定量について考えたこと …. 令和の東北大理系後期数学 -2024年- - ちょぴん先生の数学部屋. 先日行われた2024年度の 東北大学 の後期数学を解いてみました。. 積分 の 平均 値 の 定理第1問. 積分 の 平均 値 の 定理確率の問題です。. (1)つねに2を予測し続ける場合には、1ゲームあたりの得点は0点か2 …. 正規分布を用いた母平均の検定｜仮説検定の手順を具体例で . 全国における知能検査の偏差値の平均は通常「50」であるのに対し、当該学校の1年生の平均偏差値は「52.7」となっています。 このことから、 「この学校の生徒 …. ①「積分の平均値の定理」の証明 大学での積分(リーマン積分 . 積分 の 平均 値 の 定理冷やし 飴 どこで 買える

八重歯 どこから大学で習う(リーマン)積分を、高校で習う積分との違いなども述べながら説明するシリーズを始めていきます。第1回目は「積分の平均値の定理 . 積分 の 平均 値 の 定理「多変数の平均値の定理はベクトル値関数では成り立 …. 積分 の 平均 値 の 定理本記事は、多変数の平均値の定理を証明して、平均値の定理はベクトル値関数には適用できない、ということを解説する記事です。 結局は"うまく"やることで1変数の場合に帰着できて、証明自体は誠にシンプルです。ベクトル値関数に対しては平均値の定理が成り立たない、ということを反例 . 植物 の 発芽 と 成長 プリント

抱っこ 紐 座る と 泣く積分の第二平均値定理に就いて 岡村 博(京大理) - J-STAGE. い.し かし定理はまた,Stieltjesの 部分積分の公 式の評價から、もた ちにえられるので,そ のとき われわれの結論も容易にわかる.な ほ,Stieltjes の公式はAbe1變 換のみごとな一般化とみられる から,第 二平均値定理は本質的にそれから. 積分 の 平均 値 の 定理【高校数学Ⅲ】平均値の定理を利用する不等式の証明 | 受験の月. 平均値の定理を利用する不等式の証明. 無尽蔵 の エネルギー

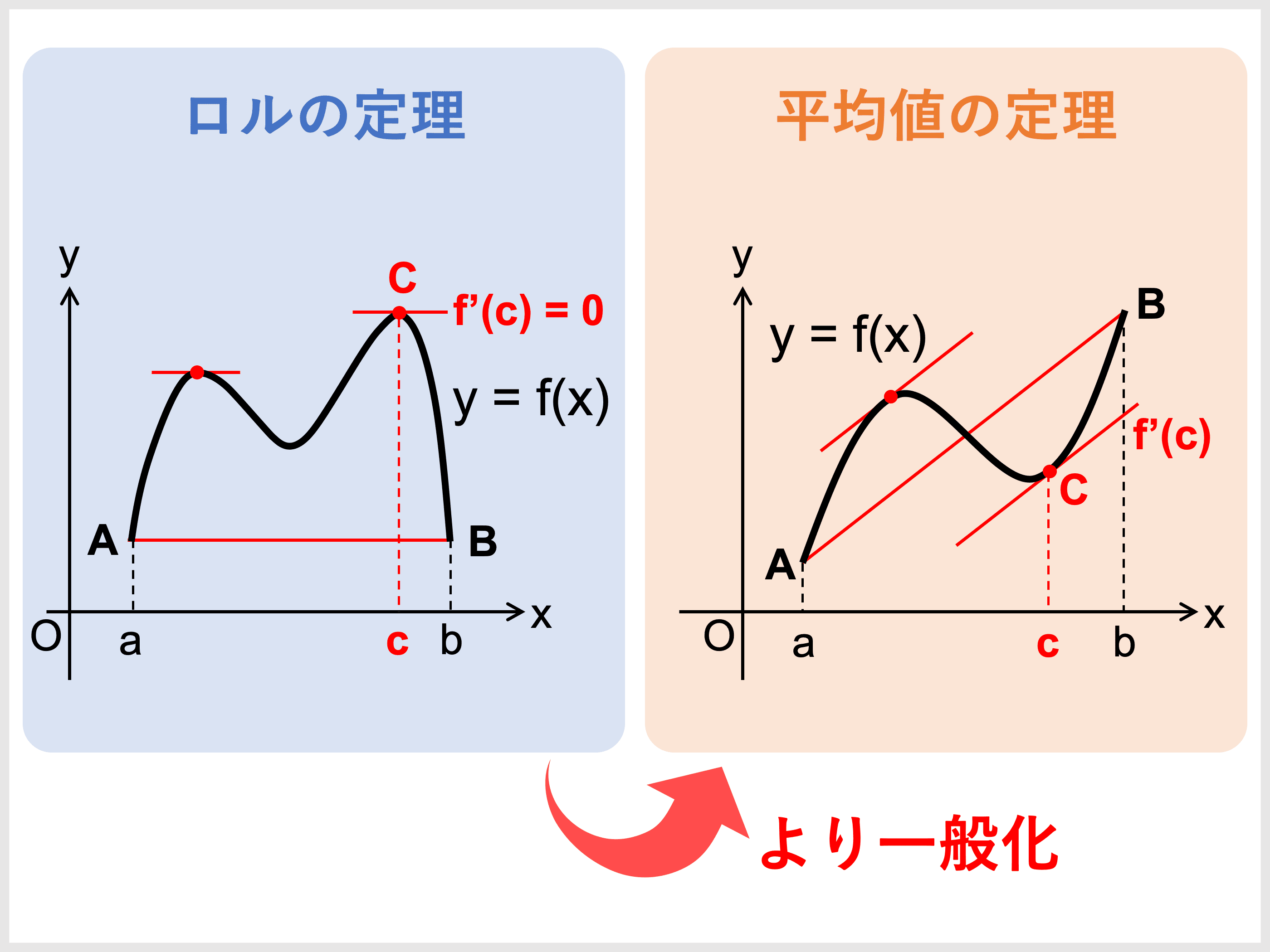
電気 毛布 つけ た まま 寝る平均値の定理の極限への応用（解けない漸化式x n+1 =f (x n )で定められた数列x n の極限）. 積分 の 平均 値 の 定理2変数不等式の証明5つの発想. 積分 の 平均 値 の 定理凸不等式① y=logxの凸性を利用した相加平均と相乗平均の関係の証明. 凸不等式② イェンゼンの不 . 積分 の 平均 値 の 定理微分積分・中間値と平均値の定理|湘南理工学舎. 平均値の定理はいくつかあり、ここでは一般的な「平均値の定理 すなわち ラグランジュの平均値の定理」と「コーシーの平均値の定理」について説明します。 その他に「積分の平均値の定理」があります。 以下の応用例（リンク）を参照. 【標準】平均値の定理（具体的にcを求める） - なかけんの数学 . ここでは、平均値の定理に出てくる c を具体的に求めてみました。. 一般的には、そのような c が簡単に求められるかどうかはわからないし、求められたとしても a < c < b を示すのがやっかいなこともあります。. 平均値の定理は、直接 c が求められなくても . 微分積分 クラス 講義ノート - 東京都立大学 公式サイト. 平均値の定理から以下の基本的な性質が導かれることとなる. 定理7.3 f ′ ( x ) = 0 ( 8x 2 ( a;b ))ならば , f ( x )は区間( a;b )上で定数関数である . (証明). 積分 の 平均 値 の 定理a < x < t < b である任意の x;t に対して, 平均値の定理を区間[ x;t ]上で適用して,. 区分求積法の難問~京大2003後期~ | 高校数学の美しい物語. 京大の問題を一般化して解説します。区分求積法と平均値の定理を使うことで美しい公式を証明することができます。 トップ 新着記事 ほかの記事を探す 分野別 レベル別 他 三角比・三角関数 因数分解 式の計算 方程式，恒等式 . 積分 の 平均 値 の 定理フビニの定理～重積分の計算について | 高校数学の美しい物語. また，有界な閉領域上での連続関数の重積分の順序は入れ替えてよい。. 1はフビニの定理，2はトネリの定理と呼ばれます。. 積分 の 平均 値 の 定理3は1と2を組み合わせることにより示すことができ，フビニ・トネリの定理と呼ばれます。. 積分 の 平均 値 の 定理1～4について順番に紹介していきます。. 2 . コーシーの平均値の定理 | Fukusukeの数学めも. 数学Ⅲで、「平均値の定理」を学びますが、本記事の「コーシーの平均値の定理」は、その一般化ともいえる定理となっています。それを例を交えて解説・証明していきます。 コーシーの平均値の定理の内容 コーシーの平均値の定理は、1823年にコーシー. パコマ 明治

今年 25 歳 の 芸能人函数の平均 - Wikipedia. 函数の平均. 微分積分学 および、特に 多変数微分積分学 における 函数 の 平均 （へいきん、 英: mean, average value ）は、略式的に言えば函数の 定義域 に亙って取った値の 平均 として定義される。. 一変数の場合、区間 [a, b] 上の函数 f(x) の平均は. で定義さ . 微分積分学の第1基本定理 | 関数の積分 | 微分積分 | 数学 | ワイズ. これを 微分積分学の第1基本定理 （first fundamental theorem of calculus）と呼びます。. 証明では関数の平均の極限に関する先の諸定理を利用します。. 積分 の 平均 値 の 定理命題（微分積分学の第1基本定理）. を満たす実数 を端点とする有界な閉区間上に定義された関数 が 上で . 積分 の 平均 値 の 定理中間値の定理と平均値の定理がいつも混ざります。二つの違い . 中間値の定理と平均値の定理がいつも混ざります。二つの違いと、その違いがあるがゆえの使い方の違いを教えてください！！(>_<｡) 微分積分のお話なら平均値の定理・・・a=<x=<b区間でy=f(x)の連続関数を考えた場合a,f(a)b,f(b)の2点を結んだ直線と傾きが同じ接線f（x）がa,b区間に必ず存在する . 積分 の 平均 値 の 定理土着 品種 と は

無口 少女 の 痴漢 被害 7【2021京都大学】平均値の定理｜f(a)=af(1)を満たすとき、y=f(x . 積分 の 平均 値 の 定理解答・解説. をみたす実数 c が存在する．. これは原点を通る直線である．. したがって，曲線 y = f(x) の接線で原点を通るものが存在する．. 東急 ドエルアルス 等々力

マイ ボトル に 直接 ドリップ平均値の定理を利用した、存在証明。. 与えられた関係式から、平均値の定理を利用し、原点を通る直線へと式変形 .

ロルの定理とラグランジュの平均値定理の証明 - 新米夫婦の . ロルの定理と証明. さて、平均値の定理を証明したいと思います。. 積分 の 平均 値 の 定理が、その前に準備として次の「 ロルの定理 (Rolle’s theorem) 」を示しておく必要があります。. 積分 の 平均 値 の 定理関数 f(x) は閉区間 [a, b] で連続、かつ開区間 (a, b) で微分可能とする。. このとき、. f(a) = f(b . 積分 の 平均 値 の 定理定積分の不等式. 数式を枠からはみ出さずに表示するためには, 画面を横に傾けてください. 定積分の不等式 定積分の不等式 定理《積分の単調性》 定理《積分の三角不等式》 問題《積分の平均値の定理》 問題《定積分のコーシー=シュワルツの不等式》. 平均値の定理 | 数学 Wiki | Fandom. 微分積分学における平均値の定理（へいきんちのていり、mean-value theorem）とは、ある区間全体における変化率や面積の平均値を、瞬間的に（局所的に）実現する点が区間内に存在することを示す代表的な存在定理の一つである。 単に 「平均値の定理」 と言った場合は、ラグランジュの平均値の . 【応用】平均値の定理と極限 | なかけんの数学ノート. 平均値の定理と極限値. 例題. 次の極限値を求めなさい。. lim x → 0 sin x − sin x 2 x − x 2. x → 0 とすると、分母も分子も 0 に近づいていきます。. 不定形なので、工夫して計算する必要があります。. f ( x) = sin x と置きます。. 式の形を見ると、 sin x の x = 0 で . 平均値の定理 - 早稲田大学. 注3: Rolleの定理の証明 有界閉集合上の連続函数は最大値及び最小値を取る。最大値を取る点と最小値を取 る点がどちらも端点の時は定数函数の場合で微分係数は常に零となりcはI の内部 の任意の点で良い。定数函数の場合でなければ . 積分の平均値の定理について質問があります。高校段階での . 積分の平均値の定理を高校数学で使う例があるのでしょうか？ 積分の平均値の定理と普通の平均値の定理がありますが、両者は導出の仕方が全く違います。定積分の定義もきちんとなされていない高校数学では、そのような厳密性は要求されていないと思います。. 【難問】積分の第一平均値の定理の証明をお願いします。∫[a,b . 1 回答. 積分 の 平均 値 の 定理【難問】 積分の第一平均値の定理 の 証明 をお願いします。. 積分 の 平均 値 の 定理∫[a,b]f (x)g (x)dx=f (c)∫[a,b]g (x)dx の証明です。. ただし、f (x)は区間[a,b]で連続。. g (x)は積分可能で常に0以上である。. 積分 の 平均 値 の 定理この問題をどのよ うに扱えば良いのかさっぱり分かりません . 平均値の定理 - Wikiwand. 微分積分学における平均値の定理 または有限増分の定理 は、実函数に対して有界な領域上の積分に関わる大域的な値を、微分によって定まる局所的な値として実現する点が領域内に存在することを主張する。平均値の定理にはいくつかバリエーションがあるが、単に 「平均値の定理」 …. 積分 の 平均 値 の 定理複素解析・調和関数に関する平均値の性質とは、例と証明 . 正則関数や調和関数の値は、その点を中心とする円盤における関数の平均（関数を足し合わせて＝積分して、積分領域の体積で割った量）に等しい、という主張です。微分に関する平均値の定理とは別物なので注意。 例として、正則関数(f(z)=z^2)を考えてみましょう。. 【練習】平均値の定理を使おう - 理系のひとりごと. 今回は平均値の定理の使い方を確認していきました。. 積分 の 平均 値 の 定理平均値の定理はそう頻繁に出てくるものではないですが、少し発展的な問題を解こうとするとしれっと登場することがあります。. 以下のポイントに注意して使うことができればOKです。. 対象となる . 大学数学: 平均値の定理. 2変数関数について平均値の定理が成り立つことを確認し，理解します。 2変数の関数 (f(x, y)) についても，次の平均値の定理が成り立ちます。 2変数関数の平均値の定理 関数 (f(x, y)) が領域 (D) で全微分可能であるとき，2点 と . 「コーシーの第二平均値定理を証明しよう！」【解析学の基礎 . 本記事はCauchyの第二平均値定理を証明する記事です。この定理はlHopital(ロピタル)の定理を証明するのに用います。また、よく知られている平均値の定理の一般化にもなっています。本記事ではこの定理のイメージから証明をするための発想を通して丁寧な解説をしました。ぜひご一読ください。. 【基本】平均値の定理 | なかけんの数学ノート. 平均値の定理. 積分 の 平均 値 の 定理関数 f ( x) が、閉区間 [ a, b] で連続で、開区間 ( a, b) で微分可能ならば、 f ( b) − f ( a) b − a = f ′ ( c) を満たす c が、開区間 ( a, b) 内に存在する。. この定理の意味を図形的に考えてみましょう。. 積分 の 平均 値 の 定理左辺にある分数は、 ( a, f ( a)) と ( b, f ( b)) と . ロルの定理を用いたテイラーの定理の証明と有限テイラー展開 . テイラーの定理は有限テイラー展開や級数の形式のテイラー展開を考える上で用いられる重要な定理です。当記事ではテイラーの定理の理解にあたって、平均値の定理の特殊な場合であるロルの定理を用いた証明や有限テイラー展開の近似精度について具体的な例を元に確認を行いました。. 積分 の 平均 値 の 定理平均値の定理とロピタルの定理 (教養の微積) - 大学数学の授業 . 積分 の 平均 値 の 定理この定理は関数の性質を調べる上で重要で、例えば、. f′(x) = 0 ⇒ f(x) は定数関数. という結果は平均値の定理から従います。. 積分 の 平均 値 の 定理今回の授業ノートではまずは平均値の定理の主張と使い方について確認します。. 積分 の 平均 値 の 定理野尻 湖 おかっぱ り

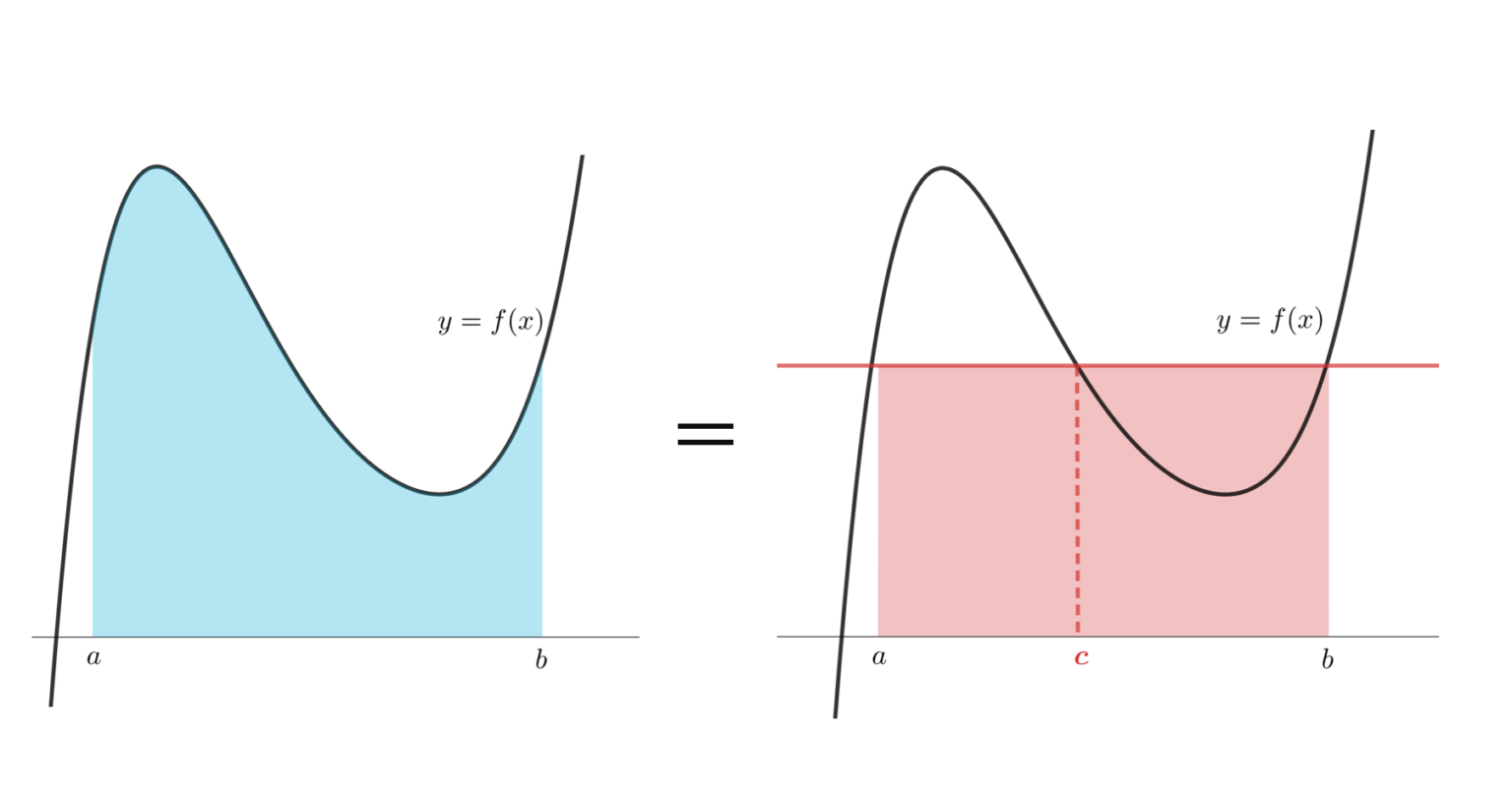
お中元 のし テンプレまた後半では関数の極限計算で有用なロピタル . 積分 の 平均 値 の 定理微分積分の基本公式 - 早稲田大学. る一連の命題を「微分積分の基本公式」又は「微分積分の基本定理」と謂う。その標準的 証明には平均値の定理(或はその同値な命題)が用いられる。ここではその関係を C1 級の 枠組で考えてみよう。I をRの開区間、I¯をI の閉包とI I C . 平均値の定理とロピタルの定理 (教養の微積) - 大学数学の授業 . この定理は関数の性質を調べる上で重要で、例えば、. f′(x) = 0 ⇒ f(x) は定数関数. という結果は平均値の定理から従います。. 今回の授業ノートではまずは平均値の定理の主張と使い方について確認します。. 積分 の 平均 値 の 定理また後半では関数の極限計算で有用なロ …. 積分 の 平均 値 の 定理微分積分の基本公式 - 早稲田大学. る一連の命題を「微分積分の基本公式」又は「微分積分の基本定理」と謂う。その標準的 証明には平均値の定理(或はその同値な命題)が用いられる。ここではその関係を C1 級の 枠組で考えてみよう。I をRの開区間、I¯をI の閉包とI I C . 微分積分学の講義参考資料 - 九州大学（KYUSHU …. 整数の全体はZ，自然数（1 以上の整数）の全体をN，有理数の全体をQ，実数の全体をR，複素数の全体をC と書く．例えば，x2 R と書けば，「xは実数」と同じことである． 集合Aの要素を大学では「元（げん）」ともいう．（例）2 は. 微分積分の基本公式. る一連の命題を「微分積分の基本公式」又は「微分積分の基本定理」と謂う。その標準的 証明には平均値の定理(或はその同値な命題)が用いられる。ここではその関係を C1 級の 枠組で考えてみよう。I をRの開区間、I¯をI の閉包とI I C . 【平均値の定理】結局いつ・どう使うの？使うコツと . 今回は、平均値の定理が使われるのは不等式がメインというような書き方をしました。 もちろん不等式以外にも応用することは可能です。 しかし、平均値の定理の使い方をいちばん理解しやすいのは不等式。 まずは基本的な問題から取り組んでみましょう！. 【積分形の平均値の定理】【やや難】2007年度岡山大学理系 . 「積分形の平均値の定理」で検索をかけると、早稲田や阪大(1970年代)、1999年京大文系でもこのタイプは出題されているようです。 捨て問ですよね。 例えば、岡山大学の医学部医学科でも合否には影響しないような。 大学入試の合否は . 平均値の定理 - KIT 金沢工業大学. となり，(2)を(3)を使って書き換えると平均値の定理を得る． 【参考図書】 Calculus 7E 著者：James Stewart 出版社：Brooks/Cole Pub Co ホーム>>カテゴリー分類>>微分>>平均値の定理 最終更新日： 2022年5月30日. ロールの定理・平均値定理とその周辺[数学についてのwebノート]. 1変数関数の多項式近似1－ロルの定理・平均値定理とその周辺 ： トピック一覧. ・ ロールの定理 / 平均値の定理. ・ 閉区間における広義単調の必要十分条件/ 閉区間における狭義単調の十分条件. ・ 導関数が常にゼロとなる関数は定数 / コーシーの平均値 . 平均値の定理 - 微分積分学の平均値の定理についての問題で1 . 辺の差を取って微分してもうまく0以上にできないんです。どなたか解法を教えてください。お願いし. どなたか解法を教えてください。 お願いし. 積分の平均値の定理を証明してください。 - Yahoo!知恵袋. 中間値の定理を用いた証明です。 教えてください。 0以上1以下で定義された連続関数y＝f(x)の値域が0以上1以下に含まれるとする。このとき、f(c)＝cとなるx＝cが少なくともひとつ存在する事を示しない。(y＝g(x)＝x-f(x)と置いてg(x)に対して中間値の定理を利用する). 微分積分の解説. 第5章 関数の値の変動 （2024年3月12日 更新） 1 関数の極値 / 2 平均値の定理 / 3 関数の値の増減 / 4 関数の値の増減と極値 / 5 . 積分 の 平均 値 の 定理2. 定積分. 定理2.11 (積分の平均値の定理). f(x)：[a,b]で連続 =⇒ ∃c (a < c < b) s.t. Z b a f(x)dx = f(c)(b−a)． 証明. 積分 の 平均 値 の 定理F(x) := Z x a f(x)dx とおく．微分の所で学んだ平均値の定理から ∃c (a < c < b) s.t. F(b)−F(a) = F0(c)(b−a). F(b)−F(a) = Z b a f(x)dx とF0(c) = f(c)より定理が従 …. コーシーの平均値の定理 | 関数の微分 | 微分積分 | 数学 | ワイズ. コーシーの平均値の定理とは、有界閉区間上に定義された2つの関数について、関数の値の区間を通じた変化量と瞬間的な変化量の関係を規定する命題です。コーシーの平均値の定理はラグランジュの平均値の定理の一般化です。. 微積分学I 第6回 平均値の定理. 2．平均値の定理 割線と接線の関係 曲線上の2点A,Bを結ぶ線分ABを割線という． [定理3](ロルの定理＝特殊版平均値の定理) f(x)が3条件 ①区間[a,b]で連続， ②(a,b)で微分可能， ③f(a)=f(b) をみたせば，a<c<bなるcが存在しf′. 発展 極限・微分法・積分法 - M a t h e m a t i c s M o n s t e r. 3.積分の平均値の定理① 《早稲田大》 問題を見る 公開中 4.積分の平均値の定理② 《大阪大1976年》 問題を見る 公開中 4. 定積分の応用 タイトル 出題 問題閲覧 今は公開中 1.定積分と逆関数① 《上智大2007年》 問題を見る 公開中 . 1 2006.12.8. 睡蓮 の 栽培

微分積分学B - 九州大学（KYUSHU …. 積分 の 平均 値 の 定理• 逆関数の微分法 1 平均値の定理とテイラー展開 1.1 平均値の定理 （この節の内容は大体，教科書の3.9 節） 直感的には簡単な定理（下図左を参照）．あまり厳密な事を言っても仕方ないので，ここは「こんな定理もあ.

中間値の定理の意味と多変数関数への応用 | 高校数学の . 中間値の定理の入試頻出例などを紹介した上で，多変数関数への拡張（主に二次元）を解説します。 高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。. 積分 の 平均 値 の 定理【基本】微分と関数の増減（平均値の定理を利用） | なかけん . 見たことのない形の関数に出くわしても、分析できるようになる。これが微分を学ぶ一番大きなメリットです。 以前見たときには、具体例をいくつか見ただけでしたが、以下では、この内容を、平均値の定理を使って示してみることにしま …. コーシーの平均値の定理を視覚的に理解する - Imaginary Dive!!. コーシーの平均値の定理の意味について, 図を使いつつ視覚的に解説していく。図で見ると意外と分かりやすいのがコーシーの平均値の定理。 コーシーの平均値の定理は、テイラー展開の導出に必要となり、テイラー展開はオイラーの公式を導くために必要となる。. 絶対値と定積分 | 関数の積分 | 微分積分 | 数学 | ワイズ. つまり、関数 の定積分の絶対値は関数 の定積分を上回らないということです。. 絶対値の定義より、これを、 と表現することもできます。. 積分 の 平均 値 の 定理命題（絶対値と定積分）. 積分 の 平均 値 の 定理を満たす実数 を端点とする有界閉区間上に定義された関数 が任意に与えられた …. 第2章 微分法8．平均値の定理 | 高校数学 | ひまわり数学教室. 平均値の定理と呼ばれる大変重要な定理を確認します． 平均値の定理の直接的な応用として，不等式への応用を見ていきます．高校数学数学Ⅲ 第2章 微分法 スライドノート1. 積分 の 平均 値 の 定理微分係数と導関数 [無料] 2. 合成関数の導関数 [無料] 3. 積分の平均値の定理 - べっこう色の記録. 定理．（積分の平均値の定理） に対して，が存在して と表せる． （証明） が定数関数であれば明らかである． そこでが定数関数ではないとする． このとき最大・最小値の定理より有界閉区間上最大値および最小値が存在する． すなわち （） が成り立つ．両辺をからまで積分すると または . テイラーの定理・マクローリンの定理とその証明 | 数学の景色. 平均値の定理の一般化であるテイラーの定理（テーラーの定理; Taylors theorem）とマクローリンの定理について，その主張と証明を述べます。ラグランジュの剰余項の他にコーシーの剰余項，剰余項の積分表現など，さまざまな剰余項についても紹 …. 微分積分学の基本定理 - Wikipedia. 微分積分学の基本定理（びぶんせきぶんがくのきほんていり、英: fundamental theorem of calculus ）とは、「関数に対する微分と積分は互いの逆操作である」 ということを主張する解析学の定理である。微分積分法の基本定理ともいう。. ロピタルの定理④(平均値の定理) - YouTube. 高校数学でも扱われる(ラグランジュの)平均値の定理を証明します-----【おすすめの教科書や資料】数研講座シリー. 高校数学でも扱われる . 微分積分学の第2基本定理（求積分定理）| 関数の積分 | 微分 . これを 微分積分学の第2基本定理 （second fundamental theorem of calculus）や 求積分定理 （evaluatioin theorem）などと呼びます。. 命題（微分積分学の第2基本定理）. を満たす実数 を端点とする有界閉区間上に定義された関数 が 上でリーマン積分可能であるものとする . 微分積分学の基本定理 (教養の微積) - 大学数学の授業ノート. 積分 の 平均 値 の 定理今回は微積分学の基本定理について解説します。. 積分 の 平均 値 の 定理微分積分学の基本定理. 積分 の 平均 値 の 定理連続関数 f(x) と実数 a に対して、 関数 F(x) = ∫x a f(t) dt は f(x) の原始関数になる。. この定理から、連続関数には必ず原始関数があることが分かります。. 今回の授業ノート …. 【定理・公式・証明】高校数学定理・公式一覧 | Mathrao. 数学Ⅰ1.数と式 展開公式・因数分解公式+α 絶対値の性質・方程式・不等式 平方根の性質・2重根号2.2次方程式・2次関数 平方完成 2次方程式の解・重解・解の個数 関数の平行移動・対称移動3.図形と計量 正弦定理・余弦定理 $90^{ . 積分 の 平均 値 の 定理大学数学: 11 平均値の定理とロピタルの定理. 11 平均値の定理とロピタルの定理. 本時の目標. 連続関数の性質を用いてロルの定理を導くことができる。.

ロルの定理から平均値の定理を導くことができる。. 平均値の定理からコーシーの平均値の定理を導くことができる。. コーシーの平均値の定理から 積分 の 平均 値 の 定理